Jämvikt
2
Jämvikt
2.1
Inledning
I detta kapitel skall vi studera jämvikten för s.k. materiella system. I ett materiellt
system kan varje del, partikel eller materialpunkt beskrivas med hjälp av dess
koordinater. Koordinatsystemet är i sin tur bundet till en referensram det s.k.
inertialsystemet eller tröghetssystemet. Definitionen av jämvikt lyder sålunda:
Ett materiellt system är i jämvikt om varje del av systemet är i vila.
Innan vi inför villkoret för jämvikt skall vi först införa begreppet inre och yttre
krafter.
snitt
S
F =mg
Rn
Yttre
krafter
Rf
Inre
krafter
F =mg
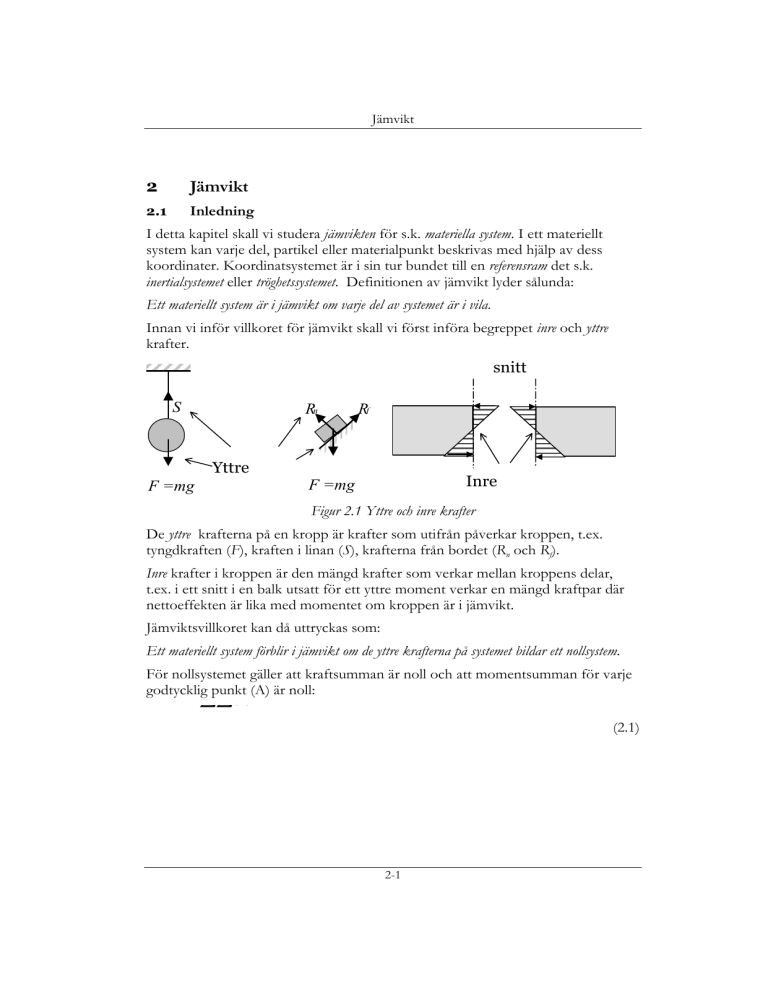
Figur 2.1 Yttre och inre krafter
De yttre krafterna på en kropp är krafter som utifrån påverkar kroppen, t.ex.
tyngdkraften (F), kraften i linan (S), krafterna från bordet (Rn och Rf).
Inre krafter i kroppen är den mängd krafter som verkar mellan kroppens delar,
t.ex. i ett snitt i en balk utsatt för ett yttre moment verkar en mängd kraftpar där
nettoeffekten är lika med momentet om kroppen är i jämvikt.
Jämviktsvillkoret kan då uttryckas som:
Ett materiellt system förblir i jämvikt om de yttre krafterna på systemet bildar ett nollsystem.
För nollsystemet gäller att kraftsumman är noll och att momentsumman för varje
godtycklig punkt (A) är noll:
0 0 A FM
(2.1)
2-1
Jämvikt
2.2
Friläggning
Det första och kanske det viktigaste steget för att bestämma jämviktsvillkoren för ett
materiellt system är den procedur som kallas friläggning där man ritar ut de yttre krafter som
verkar på kroppen. OBS! inga andra krafter får förekomma i figuren. Vi skall först studera
ursprunget för några vanliga typer av kontaktkrafter.
Typ av kontakt eller ursprung
Friläggning
Flexibel lina, vajer, band eller rep
En kraft som
kommer från en
flexibel lina är
alltid en dragkraft
egenvikt försummas
egenvikten påverkar
Rå yta
Slät
yta
Slät yta
Fast inspänd
Ledad
Rullstöd
Rå yta
Ett fast inspänt stöd tar
upp moment (M) och
krafter i två riktningar
(F, V).
Led rörlig fixerad
Rullstöd
Egentyng
d
Fjäder
Fjäderkraften ger tryck om den
komprimeras och drag om den
tänjs ut. En linjär fjäder ger en
kraft direkt proportionell mot
förlängningen (F=kx)
2-2
Jämvikt
En annan viktig aspekt vid friläggning är det system man skall studera. Här kan
man tillämpa Newtons lag om verkan och motverkan:
Mot varje kraft svara en annan lika stor och motsatt riktad kraft, så att de ömsesidigt mellan
två kroppar verkande krafter är lika stora och motsatt riktade.
Beroende på om vi betraktar jämvikten för mannen eller välten i Figur 2.1 får vi
två olika system att frilägga.
System
1
System
2
Figur 2.1 Friläggning av system
2-3
Jämvikt
Arbetsgången vid friläggning av ett system kan sammanfattas med följande
punkter:
Bestäm vilket eller vilka system/delsystem som skall friläggas. Valet
innehåller ofta ett eller flera obekanta storheter.
Isoleringen av systemet görs vid definierade gränser t.ex. kontaktytor eller
gränser till andra attraherande/repellerande kroppar.
Kontaktytor, attraherande kroppar, egentyngd m.m. ersätts med inritade
krafter. Kända krafter inritas med angiven av kraftens storlek och riktning.
Okända krafter skall representera med kraftpilar i en antagen riktning
(helst i enlighet med det valda koordinatsystemet). Beräkningarna
kommer sedan att visa om riktningen är korrekt eller motriktad (negativt
värder).
Valet av koordinatsystem bör också anges i figuren.
Exempel:
System
Frilagt system
Fackverk
egenvikten är
försumbar
Fast inspänd balk
Ledad infäst balk
Underlaget vid A är
glatt, dvs. stödkraft är
riktad normalt balken
2-4
Jämvikt
2.3
Jämviktsekvationer
I det allmänna fallet kan tre stycken oberoende jämviktsekvationer ställas upp i ett
2 - dimensionellt koordinatsystem:
F
x
0, Fy 0, M z 0
(2.2)
dvs. summan av alla krafter i x respektive y riktningen samt summan av
momenten runt en godtycklig punkt skall vara noll. Beroende på kraftriktningar
och position kan antalet oberoende jämviktsekvationer reduceras.
Kraftsystem
Exempel
Alla krafter har gemensam
verkningslinje. Antalet
jämviktsekvationer = 1
Alla krafters verkningslinjer
passerar genom en gemensam
punkt.
Antalet jämviktsekvationer = 2
Parallellt kraftsystem. Antalet
jämviktsekvationer = 2,
en kraft och en momentekvation.
Generellt 2 dimensionellt system.
Antalet jämviktsekvationer = 3
2-5
Jämvikt
Exempel 2.1
Beräkna krafterna C och T i figuren till
vänster.
Lösning:
Fx 0 :
8 T cos 40 C sin 20 16 0
0.766T 0.342C 8
F
y
0:
T sin 40 C cos 20 3 0
0.643T 0.940C 3
Genom att kombinera de två
ekvationerna kan vi lösa ut C och T
Svar: T 9.09 kN C 3.03 kN
Exempel 2.2
Bestäm storleken på kraften T i kabeln
som håller upp balken. Balken har en
egenvikt på 95 kg per meter.
Lösning:
Frilägg figuren och ansätt egentyngden
på balken ( 95 9.81 5 46600 ) i
mitten. Genom att ta en moment
ekvation runt punkten A, kan T lösas
ut direkt:
M A 0 (vridning moturs positiv)
T cos 25 0.25 T sin 25 5 0.12
Alla krafter går genom en gemensam punkt,
dvs. vi kan utnyttja två jämviktsekv:
Fx 0, Fy 0
Frilagt system
10 5 1.5 0.12 4.66 2.5 0.12
0 Svar: T 19.61 kN
Övning: Beräkna Ax , Ay från
F F
x
y
0.
Svar: Ax 17.77 kN, Ay 6.37 kN
2-6
Jämvikt
2.4
Tyngdpunkt, masscentrum, statiskt moment, yttröghetsmoment
En viktig kraft som alltid förekommer i alla system är egentyngden. Ibland kan
inverkan av egentyngden vara försumbar och behöver ej beaktas i friläggningen. I
de fall den tas med är det viktigt att kunna bestämma kroppens tyngdpunkt, dvs.
den punkt i kroppen där tyngdkraftens verkningslinje passerar. Denna punkt
sammanfaller med kroppens masscentrum.
2.4.1 Masscentrum för partikelsystem
ri
mi g
r
mi g
mi g
mg
0
mi g
mi g
mi g
Figur 2.2 Partikelsystem
Betrakta ett partikelsystem som består av ett antal individuella partiklar var och en
med massan mi .Varje partikel i systemet påverkas av en tyngdkraft mi g vars
riktning är lika för alla partiklar i systemet Vi vet från tidigare kapitel att vi kan
ersätta alla delkrafter med en resultant vars belopp blir:
R mi g mg
(2.3)
i
Resultantens angreppspunkt bestäms av de faktum att delpartiklarnas
momentsumma måste överensstämma med resultantens moment:
rm g rm
i
r R ri mi g r
i
i
mg
i
i
i
m
i
(2.4)
där ri är avståndet från en godtycklig referenspunkt 0. Ovanstående kan delas upp
genom att betrakta varje koordinat för sig så att:
x
m x
i i
i
m
,y
m y
i
i
m
i
,z
m z
i i
i
m
2-7
(2.5)
Jämvikt
dvs. angreppspunkten, masscentrum, tyngdpunkt1 för ett partikelsystem kan uttryckas
som summa av alla partiklars massa multiplicerat med avståndet från origo
dividerat med den totala massan av alla partiklar. Termen mi ri brukar
i
betecknas som det statiska momentet m a p ett visst plan:
S yz mi xi , S xz mi yi , S xy mi zi
i
i
(2.6)
i
d v s masscentrum eller tyngdpunkten för ett partikelsystem kan uttryckas som:
x
S yz
m
,y
S
S xz
, z xy
m
m
(2.7)
2.4.2 Masscentrum för volymer
För kroppar som har en kontinuerlig massfördelning övergår ovanstående
summor till integraler.
(x,y,z)
dm
z
r
x
y
Figur 2.3 Kontinuerlig massfördelning för volymer
Om kroppens densitet betecknas med [kg/m3] kan den uttrycket för kroppens
massa skrivas m dm dV där integralen är en volymsintegral. Uttrycken för
V
de statiska momenten övergår på motsvarande sätt till volymsintegraler, t ex så
blir det statiska momentet m a p yz planet S yz x dm x dV o s v. För
V
specialfallet när densiteten är konstant sammanfaller kroppens masscentrum med
volymens tyngdpunkt, d v s:
x
1
S Vyz
V
xdV
V
V
ydV
V
zdV
S xy
S xzV V
V
,y
,z
V
V
V
V
I ett homogent tyngdkraftsfält sammanfaller masscentrums koordinater med tyngdpunkten
2-8
(2.8)
Jämvikt
V
där V är kroppens volym och t ex S xy
betecknar volymen statiska moment m a p
xy-planet.
2.4.3 Masscentrum, tröghetsmoment för ytor
För kroppar med konstant tjocklek t i en riktning, t ex, skal kan uttrycket för
masscentrum förenklas genom att volym och volymsintegraler kan ersättas med
area och areaintegraler:
x
S yzA
A
xdA
A
S xzA
,y
A
A
ydA
A
A
,z
t
2
(2.9)
där A är skalkroppens area och t ex S yzA betecknar areans statiska moment m a p
yz-planet. Normalt brukar man beteckna areors statiska moment med:
S y xdA, S x ydA
A
(2.10)
A
d v s man anger inte z koordinaten
Figur 2.4 Kontinuerlig massfördelning för ytor
2-9
Jämvikt
En annan viktig storhet som har stor praktisk betydelse i mekaniken, speciellt när
det gäller balkteori är ytors tröghetsmomentet. Ytors tröghetsmoment definieras som:
I x y 2 dA, I y x 2 dA
A
(2.11)
A
Rent praktiskt kan man tolka tröghetsmomentet som de moment som en linjärt
varierande ytlast ger på en area runt en specifik axel. Vi kan på ett enkelt sätt
paralellförflytta tröghetsmomentet m h a Steiners sats.
y0
(x,y)
x0
TP
y
r
A
x
Figur 2.5 Steiners sats
Låt oss säga att vi har beräknat tröghetsmomenten I x 0 och I y 0 för kroppen i
Figur 2.5 d v s med avseende på axlarna x0 och y0. som skär kroppens tyngdpunkt.
Nu vill vi beräkna tröghetsmomenten m a p axlarna x och y d v s parallellförflytta
tröghetsmomentet till en ny axel. Steiners sats innebär att det nya
tröghetsmomentet fås genom att addera avståndet från tyngdpunkten i kvadrat
gånger kroppens area, A:
I x I x0 y 2 A
(2.12)
I y I y0 x2 A
Storheter som tyngdpunkt, statiskt och yttröghetsmoment finns tabellerade för
olika geometrier i Appendix 1. Genom att använda Steiners sats kan man sedan på
ett enkelt sätt parallellförflytta tröghetsmomentet till önskad position.
2-10
Jämvikt
2.4.4 Exempel
Exempel 2.3
Beräkna tyngdpunkten för den tunna
homogena kroppen till höger.
y
a/2
Lösning:
x1 a 2, y1 a 2
Del 1:
A1 a 2
2
a/4
a/2
a
a2 a
a 4 9a
, y2 a
2
4
2
8
Del 2:
2
aa a
A2
24 8
1
x2
Del 3:
4a / 2 a(3 2)
a
, y3
3
3
2
x3 a
a
a 2
A3
2 2
8
2
Summor:
Ax
i
i
A1 x1 A2 x 2 A3 x3
i
3
x
a
Tyngdpunkten beräknas genom först ta fram
tyngdpunkterna för de ingående delarna. Sedan
summeras bidragen p s s som ett system av
partiklar. På grund av att densiteten och
tjockleken t är konstant kan uttrycket
reduceras t.ex. för x-koordinaten till:
x
m x
i i
i
m
t Ai xi
i
t Ai
i
Ax
A
i i
i
i
i
a 2 a a 2 a a 2 a(3 2)
1.007a 3 OBS!
2
84
8 3
Kontrollera om svaren verkar rimliga
i Ai yi A1 y1 A2 y 2 A3 y3
a 2 a a 2 9a a 2 a
0.837a 3
2
88
42
A
i
i
A1 A2 A3
a 2 a 2
a
1.518a 2
8
8
2
Ax
A
Ay
y
A
x
i
i
i
i
1.007a
0.664a
1.518a 2
i
0.837a 3
0.551a
1.518a 2
i
i
i
i
i
2-11
Jämvikt
Exempel 2.4
y
Alla som har böjt på en bräda vet att
den blir mycket styvare om man ställer
den på högkant. Det beror på att
tröghetsmomentet blir mycket större
när brädan står på högkant jämfört om
den ligger ned. Vi skall i det här
exemplet bestämma tröghetsmomentet
I x runt x-axeln för en I-balk genom att
använda Steiners sats.
2
x
1
3
Lösning:
Mått för del 1, 2 och 3
Bestäm först tröghetsmomentet för
delarna var för sig:
40 mm
400 mm
bh3 40 4003
2.133 108 mm
12
12
400 403
I 2 I3
2.133 106 mm
12
I1
Använd sedan Steiners sats för att
förflytta del 2 och 3 till var sin kant av
del 1:
x0
h
b
I x I1 I 2 A2 y I 3 A y
2
2
1
2,3
2
3 3
2.133 108
Enligt appendix 1: I x 0
2 2.133 106 400 40 2202
1.766 109 mm
2
Svar: 17.66 108 mm
Vi ser att del 2 och 3 tröghetsmoment
runt axeln x0 är försumbart jämfört med
bidraget från Steiners sats.
1
x0
400/2+40/2
x
220 mm
3
2-12
bh3
12
x0
Jämvikt
2.5
Övningsuppgifter
Uppgift 2.1
Rita in de krafter som saknas i friläggningsskissen till höger
2-13
Jämvikt
Uppgift 2.2
Bestäm med vilken horisontell kraft P
trädgårdsmästaren till höger måste
skjuta på den 100 kg tunga välten.
Bestäm också reaktionskraften R som
verkar mellan mark och vält. Vältens
tyngdpunkt är vid punkten 0.
Svar: P =173.0 N, R = 996 N
Uppgift 2.3
Vilken horisontell kraft P måste mannen
på bilden dra med för att placera den 50
kg tunga lasten mitt över lastbilen.
Svar: P = 126.6 N
2-14
Jämvikt
Uppgift 2.4
Ringen som sitter upphängd med två
kablar fästa i de vertikala väggarna är
belastad med kraft på 1000 N. Beräkna
krafterna som uppstår i kablarna, T1 och
T2.
Svar: T1 = 897 N, T2 = 732 N
Uppgift 2.5
Bestäm vinkeln så att den applicerade
kraften P placerar den 250 kg lasten mitt
över öppningen. Bestäm också
linkraften T på den 3.9 m långa linan.
Svar: = 44.8 O, T = 4.53 kN
2-15
Jämvikt
Uppgift 2.6
Kabeln mellan A och B är 6 m lång och
håller upp en 100 kg tung låda. Bestäm
kraften T (drag) i kabeln.
Uppgift 2.7
Skruven vid B har dragits åt så mycket
att träblocken är under en tryckkraft av
500 N. Vad är då kraften som verkar i
skruv A? (Antag att krafterna som tas i
de båda skruvarna är i skruvens
riktning).
Svar: A = 1250 N.
Uppgift 2.8
Verktyget används vid limning för att
pressa ihop ett laminat på var sin sida
nära kanten. Om en kraft på 120 N
appliceras på handtaget, vilken blir då
kraften som rullarna pressar på
laminatet?
2-16
Jämvikt
Uppgift 2.9
Bestäm kraften T i storlek av massan m
som hänger i systemet av block.
Försumma egenvikten av taljor och
block.
Uppgift 2.10
Om man placerar en distans under
huvudet på en hammare ökar man
avsevärt kraften för att dra ut spikar.
Bestäm dragkraften T på spiken och
tryckraften som verkar vid punkten A
om man applicerar en kraft på 200 N i
skaftet på hammaren i figuren till höger.
Kontaktytan är tillräcklig rå för att
förhindra att hammaren glider.
Svar: T = 800 N, A = 755 N.
Uppgift 2.11
En 200 kg tung balk med tyngdpunkten
vid G sitter fastsvetsad i en pinne som
går genom punkten A. För att prova
svetsen vid A ställer sig en 80 kg man
och drar med en kraft av 300 N i ett
rep. Beräkna momentet M som
påverkar pinne vid A.
Svar: M = 4.94 kNm
2-17
Jämvikt
Uppgift 2.12
Kranen lyfter en 4.20 ton tung truck.
Masscentrum av den 2 ton tunga
lyftbommen OA är placerad mitt mellan
i punkten O och A. Beräkna dragkraften
i vajern T som sitter fast i punkten B
och storleken på reaktionskraften vid O
som verkar i riktning av bommen OA.
Svar: T = 61.5 kN, O = 99.2 kN
Uppgift 2.13
En trumma som väger 400 kg ligger på
rullar vid A och B. Rullen vid A är fri
att röra sig friktionsfritt. Rullen vid B
måste påföras en friktionskraft i
tangentens riktning mellan kontakten
trumma - rulle innan den börjar röra sig.
Beräkna friktionskraften F om
friktionsmotståndet övervinns precis
när mannen står vid positionen visad i
figuren. Mannen väger 80 kg.
Svar: F = 816 N
Uppgift 2.14
Den homogena balken i figuren är 6 m
lång och väger 300 kg. Lyftanordning
används att lyfta balken. Vad är kraften i
repen AC ( TA )och BC ( TB ) när balken
lyfts av stöden?
Svar: TA 816 N, TB 2450 N
2-18















