Kleindagarna2013,IML,Stockholm,14-16juni2013
Att skala om, att mäta och att avbilda avstånd
Jana Madjarova, Matematiska vetenskaper, Chalmers/GU
Det kommer nog inte som någon större överraskning att omskalning och likformighet är
nyckelbegrepp när det handlar om att avbilda det tredimensionella rummet på ett platt papper och om
perspektiv. Däremot kanske man kan bli fundersam över hur skala och likformighet kan hänga ihop
med begreppet area, och därmed även med begreppet volym. Här påminner vi om de viktigaste
satserna om kongruens och likformighet för trianglar och reder ut kopplingen till triangelns area.
Sedan tittar vi på hur man kan använda omskalning för att, om inte bevisa stringent, så åtminstone
troliggöra area- och volymformler. Till sist vänder vi blickarna mot perspektivet som ett sätt att skapa
”rätt” tvådimensionell bild av den tredimensionella verkligheten och avslutar med att diskutera hur
man kan använda geometrins koppling till konsten i sin undervisning.
Kongruens och likformighet – definitioner och viktiga satser
För att inte gräva ner oss i axiomatiken för geometrin kommer vi att ge en ganska handgriplig
definition av kongruens1: två figurer är kongruenta om man kan flytta den ena (eventuellt får man
lämna planet för att göra det) så att den helt sammanfaller med den andra. Två trianglar är kongruenta
om och endast om motsvarande sidor är lika långa och motsvarande vinklar är lika stora. I själva
verket räcker likhet mellan färre element, vilket är innehållet i de så kallade kongruensfallen.
Första kongruensfallet: Om , , och ∠ ∠′, så ∆ ≌ ∆ . (s-v-s)
Andra kongruensfallet: Om , , och ∠′′, så ∆ ≌ ∆ . (s-s-s)
Tredje kongruensfallet: Om , ∠ ∠′, och ∠ ∠′, så ∆ ≌ ∆ . (v-s-v)
Många gånger klarar elever och studenter av att fastställa att två trianglar är kongruenta enligt något av
fallen, men vet inte riktigt hur de ska använda kongruensen. Poängen är att om tre element av rätt sort
(som beskrivet i något kongruensfall) är lika, så är resterande tre element också lika. Om till exempel
∆ ≌ ∆ enligt första kongruensfallet som ovan, så följer ur detta att , ∠ ∠′, och ∠ ∠′. I själva verket följer mer än så, alla motsvarande element i de båda trianglarna
måste vara lika (höjder, medianer, bisektriser, etc.). Vilka element är då ”rätt”, finns det till exempel
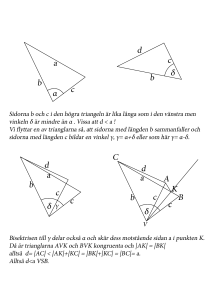
inget s-s-v-fall? Generellt gör det inte det, vilket illustreras av exemplet nedan:
1
Kongruens är i själva verket ett primitivt begrepp som inte definieras, utan vars uppförande styrs av ett antal
s.k. kongruensaxiom.
1
Det finns en sats som ofta kallas ”fjärde kongruensfallet”, som säger att s-s-v räcker, om vinkeln är
mot den större av sidorna. Satsen är mycket användbar när man ska visa att två rätvinkliga trianglar är
kongruenta, eftersom den räta vinkeln alltid är störst.
Likformighet handlar istället om proportioner. Man skulle kunna säga att två figurer är likformiga om
en av dem kan flyttas och skalas om så att den sammanfaller med den andra.
Definition. Två trianglar är likformiga om motsvarande vinklar är lika stora och motsvarande sidor
förhåller sig till varandra på samma sätt, det vill säga, ∆~∆′′′ om ∠ ∠′, ∠ ∠′,
∠ ∠′, och
.
Tre (eller fyra, om man vill se det så) likformighetsfall gäller, som exakt motsvarar kongruensfallen,
den enda skillnaden är att likheter mellan sidlängder ersätts av proportioner. Det tredje fallet
omvandlas till v-v, eftersom man inte kan ha proportion när det bara handlar om ett par motsvarande
sidor. Bevisen bygger på två grundläggande satser, transversalsatsen och topptriangelsatsen. I båda
dessa spelar parallellitet en avgörande roll. Det torde därför inte komma som en överraskning att
likformighet (till skillnad från kongruens) är ett genuint euklidiskt begrepp.2
Frågor att diskutera:
o
o
o
o
o
o
Varför fungerar inte motexemplet från figuren ovan under förutsättningarna för ”fjärde
kongruensfallet”?
Finns det ett v-v-s-fall?
Om två trianglar är kongruenta (likformiga) med en tredje, är de då kongruenta (likformiga)
sinsemellan?
Givet en triangel, ∆, som utgångspunkt, hur många principiellt olika figurer kan man rita
för att illustrera topptriangelsatsen?
Är omvändningarna till transversalsatsen och topptriangelsatsen sanna?
Varför kan man inte bevisa topptriangelsatsen med hjälp av det tredje likformighetsfallet?
Vad är längd, area och volym, och hur kan man mäta och beräkna dem?
Vi börjar med att ”härleda” den välkända formeln för triangelns area med hjälp av omskalning. Titta
på trianglarna och i figur 1, där ||. De är likformiga enligt topptriangelsatsen. Om
sidlängden i den lilla triangeln förhåller sig till sidlängden i den stora som till 1, där < 1, så
kommer den lilla arean att förhålla sig till den stora som till 1. Vi har att arean av den stora
triangeln är lika med arean av den lilla plus arean av det avskurna parallelltrapetset. För nära 1
kommer parallelltrapetsets area att vara ungefär lika med arean av rektangeln ′′, och vi får att
≈ + ∙ 1 − ℎ, vilket ger 1 + ≈ ℎ, där är längden av sidan och ℎ är längden av
höjden . Om vi nu låter närma sig 1, får vi att =
!
.
Ordet härleda stod inom citationstecken ovan. Så varför är inte härledningen ovan riktigt stringent?
Kan vi fylla i luckorna och göra den stringent? Till att börja med måste vi identifiera dessa luckor. Här
är de frågor som måste ställas:
•
•
•
2
Hur vet vi förhållandet mellan areorna om vi inte kan någon formel för dem?
Vad betyder ”ungefär lika med”?
Vad betyder ”närma sig”?
Om två trianglar i hyperbolisk geometri har lika vinklar, så är de kongruenta (”femte kongruensfallet”).
2
Och så de frågor som kanske är svårast att komma på att man måste ställa:
•
•
Hur vet vi att en triangel överhuvudtaget har en area?
Vad är area?
Figur 1
Areafunktionen är en funktion från en delmängd av mängden av figurer i planet till mängden av ickenegativa reella tal sådan att kongruenta figurer har lika areor, och om en figur är unionen av (d.v.s.
består av) två figurer med tomt snitt (d.v.s. som inte överlappar), så är dess area summan av de två
delfigurernas areor. En kvadrat med sidlängd 1 längdenhet har area 1 areaenhet. Frågan om en mängd
har area eller inte är inte alls lätt att besvara. Till och med för att härleda formeln för en rektangels area
krävs ett egentligen ganska avancerat kontinuitetsargument. Mängder som har en area kallas
kvadrerbara.
Likformighet är ett genuint euklidiskt begrepp. Kan det då vara så att ”härledningen” har ytterligare an
subtil brist, att vi tagit fram formeln för triangelns area under onödigt starka förutsättningar? Svaret på
den frågan är nej, formeln !
är i sig euklidisk och bygger på likformighet. För att övertyga oss
om det noterar vi att om den gäller, så måste den rimligen gälla oavsett vilken av triangelns sidor vi
väljer som bas. I de vedertagna beteckningarna måste det alltså vara sant att "# , det vill säga
(se figur 2)
$
. Att detta gäller följer ur att ∆ ~∆ C, enligt tredje likformighetsfallet.3
$
Figur 2
3
En triangels area i hyperbolisk geometri definieras som % − & + ' + (, där &, ', ( är triangelns vinklar.
3
Låt oss titta lite på de övriga frågorna vi ställde. ”Närma sig” handlar naturligtvis om gränsvärde, en
fråga som tas upp i gymnasiekurserna. Det räcker här att behandla den ganska intuitivt. ”Ungefär lika
med” är samma som att säga att felet vi gör vid det beskrivna förfarandet är försumbart. Naturligtvis
infinner sig då frågan, vad är försumbart? Lite löst talat är en term att betrakta som försumbar om den
är ordningsmässigt mindre än alla termer som tagits med. I vårt exempel har vi vid approximationen
av parallelltrapetset med en rektangel gjort ett fel som motsvarar arean av de två små trianglarna
och ′ i figur 1. Den minsta termen som är med är bottenrektangelns area. Dess ”litenhet”
kommer sig av den lilla höjden den har, som är 1 , så den är liten av ordning 1 . De små
trianglarnas areor är däremot små av ordning 1 , då både bas och höjd är av ordning 1 .
Du kan använda samma argument som ovan för att, om inte härleda, så åtminstone troliggöra formeln
för en kons volym, ) !
.
*
Ersätt den avskurna tunna bottenplattan (se figur 3) med en rak cirkulär
cylinder och imitera det tidigare förfarandet.
Figur 3
Frågor att diskutera:
o
o
o
o
o
o
o
o
o
Vad är längd, area och volym, alltså mått i en, två och tre dimensioner?
Kan man, och i så fall hur, ”handgripligen” mäta längd? Area? Volym?
Vad är att betrakta som försumbart? Exempel från fysiken?
Grafiskt: approximera en funktions graf med tangenten i närheten av en punkt. Är den en bra
approximation?
I figur 4 nedan, varför är längden av den kantiga linjen +,-. … 0 en dålig approximation av
sträckan :s längd oavsett hur fin indelning vi väljer, medan arean under den kantiga linjen
är en bra approximation av hela triangelns area?
Arkimedes princip: hur kan man härleda formeln för konens volym med hjälp av inskrivna
cylindrar?
Hur skulle man kunna definiera ett fyrdimensionellt rätblock? En fyrdimensionell kon? Vad
borde de ha för (fyrdimensionell) volym?
Ett par av frågorna ovan kan faktiskt ses som en introduktion till integralräkning. Vilka
handlar det om?
2
Om & = ' + (, där & 1 ', är det alldeles säkert att = 345?
4
Figur 4
En enögd basketspelare med kubistiska ögon spelar schack
Under Renässansen utvecklades geometrin av konstnärer som Piero della Francesca och Albrecht
Dürer, snarare än av professionella matematiker. En av anledningarna var ansträngningarna att avbilda
den tredimensionella verkligheten på plan duk så att avbildningen ser ”rätt” ut. Som rubriken och
citationstecknen antyder ska rätt tas med en nypa salt. Även efter att man kommit underfund med hur
parallella linjer avbildas, med försvinningspunkter och horisontlinje, återstår ett stort problem,
nämligen att få det riktiga djupet i bilden. Inte helt överraskande löser man det problemet med hjälp av
likformighet. Nedan följer en inlämningsuppgift ur kursen Rum och geometri för åk 1 på programmet
Arkitektur och teknik, Chalmers, och lösningen som Pedram (AT’07) gav. Lösningen ger en ledtråd
till en av förutsättningarna för att bilden ska se rätt ut.
En 2,15 m lång (enögd) basketspelare med ögonhöjd 2 m står 3 m ifrån ett golvschackbräde med
måtten 2x2 m. Hur skulle han avbilda schackbrädet på en duk som står vertikalt i den av brädets kanter
som befinner sig närmast basketspelaren? Motivera väl!
Ett problem man måste lösa är att dela in bilden av schackbrädet i smårutor som ser att vara lika stora i
verkligheten. Det är lättgjort eftersom åtta är en potens av två och det är lätt att halvera. Figurerna
5
nedan visar hur man kan modifiera det välkända förfarandet4 att dela in en sträcka i ett antal lika länga
delar till en variant som gäller i perspektiv. När vi delar in bilden av rektangeln i 25 lika stora
smårektanglar är det väsentligt att vi ser dess främre sida rätt; annars får man utföra indelningen i två
steg.
Uppgiften som illustreras av den figur 5 är följande:
Givet ett parallelltrapets, visa att linjen genom diagonalernas skärningspunkt och skärningspunkten för
de två icke-parallella sidornas linjer går genom de två parallella sidornas mittpunkter.
Uppgiften kan lösas direkt (det finns ett stort antal likformiga trianglar inblandade), men den kan
också tolkas som bilden av en rektangel i perspektiv. Påståendet blir då mer eller mindre uppenbart.
Det kan tyckas vara en mindre matematisk lösning, men, i själva verket är den fullständigt legitim. Det
är en uppgift från ett prov i kursen Rum och geometri. Eftersom den är ganska svår var det inte alla
4
som givetvis bygger på likformighet …
6
som löste den, men av dem som gjorde det valde ungefär hälften den andra lösningen. Man skulle
kunna säga att de använde projektiv geometri utan att veta om det.
Figur 5
Matematik uppfattas ofta som ett tråkigt ämne och förknippas sällan med allmänbildning. Att referera
till konstnärer som bidragit till geometrins utveckling och att visa hur ren geometri kommer till
användning i konsten kan vara ett bra sätt höja intresset för ämnet. Det är inspirerande och roligt för
klassen att få se bilder av Piero della Francesca, Dürer, Escher, och att få höra något om Brunelleschi,
katedralen i Florens och utvecklingen av perspektivet.
En klassisk sats och några problem
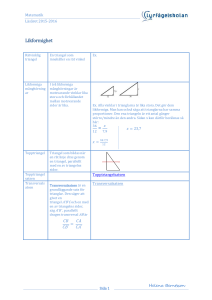
Vi börjar med en av den euklidiska geometrins klassiska satser. Beviset som återges här bygger på
likformighet. Dessutom illustrerar det hur man använder de viktiga satserna om likformighet och deras
omvändningar.
Sats. De tre medianerna i en triangel skär varandra i en punkt (triangelns tyngdpunkt).
Bevis. Låt vara en triangel, och beteckna med , resp. mittpunkterna på sidorna , resp. . Trianglarna och är likformiga (s-v-s). Sträckan är parallell med (enligt
omvändningen till topptriangelsatsen), och hälften så lång, eftersom : = : = 1: 2.
(Alternativt kan man använda omvändningen till transversalsatsen.) Beteckna med 0 punkten i vilken
medianerna och skär varandra. Trianglarna 0 och 0 är nu likformiga, enligt
7
topptriangelsatsen, och 0: 0 0: 0 : 2: 1. Det innebär att punkten 0 delar var
och en av de två medianerna i förhållande 2: 1, räknat från hörnet. Det följer att 0 även ligger på den
tredje medianen (varför?).
1. Dela en sträcka i ett givet antal lika delar.
2. Visa att höjden mot hypotenusan i en rätvinklig triangel delar triangeln i två trianglar, båda
likformiga med den ursprungliga.
3. Givet ett parallelltrapets 8, ||8, visa att sträckan som sammanbinder mittpunkterna
på sidorna och 8 är parallell med och 8, samt att dess längd är det aritmetiska
medelvärdet av deras längder.
4. Givet ett parallelltrapets 8, ||8, visa att sträckan parallell med och 8, som har
ändpunkter på de två andra sidorna, och som passerar genom diagonalernas skärningspunkt 9,
delas på mitten av 9.
5. Givet är två trianglar med gemensam bas, lika höjder till den och som ligger på samma sida
om basen. En rät linje är parallell med trianglarnas bas och skär deras återstående sidor. Visa
att sträckorna, som de båda trianglarnas sidor skär av linjen, är lika långa.
6. Härled en formel för parallelltrapetsets area.
7. Visa att den regelbundna åttahörningens area är lika med produkten av dess längsta och dess
kortaste diagonal. Försök hitta flera olika bevis.
8. Vad ska en fyrhörning uppfylla för att dess area ska vara lika med produkten av dess båda
diagonallängder? (Ledtråd: Titta på några specialfall.)
9. (Svår) Givet en spetsig triangel, visa att den är likformig med triangeln med hörn i
fotpunkterna till höjderna från två av hörnen och i det tredje hörnet. Hur ser det ut om
triangeln inte är spetsig?
10. (Svår) Visa att höjderna i en spetsig triangel är bisektriser till vinklarna i triangeln med hörn i
fotpunkterna till höjderna i den givna triangeln. Hur ser det ut om triangeln inte är spetsig?
8